hi, i'm nathan ng

While doing some background reading on positive definite kernels and Reproducing Kernel Hilbert Spaces (RKHS) I found that many definitions were a bit hard to understand intuitively. This is my own attempt at explaining these concepts, mainly to solidify my own knowledge but also to share with others. Much of this was based on Arthur Gretton’s Introduction to RKHS and this excellent paper on a generalized representer theorem by Scholkopf, Herbrich and Smola. $ \def\bw{\mathbf{w}} \def\bx{\mathbf{x}} \def\by{\mathbf{y}} \def\bz{\mathbf{z}} \def\RR{\mathbb{R}} \def\H{\mathcal{H}} \def\X{\mathcal{X}} \def\wc{\mkern 2mu\cdot\mkern 2mu} $

XOR: A Motivating Example

Linear model are a useful class of models that combine input dimensions linearly (i.e. via inner products) to compute an output. One common linear model for performing binary classification is a Support Vector Machine (SVM), which attempts to learn the a separating hyperplane $\bw^\intercal \bx = 0$ parameterized by $\bw$ between the two classes of data points. Classification can then be performed on a test input $\bx$ by computing $\bw^\intercal\bx$ and thresholding at $0$. For convenience we assume the bias term has been absorbed into the input $\bx$.

SVMs work well only when data is linearly separable, which is not always the case. Consider the problem of learning the XOR function, depicted below ¹:

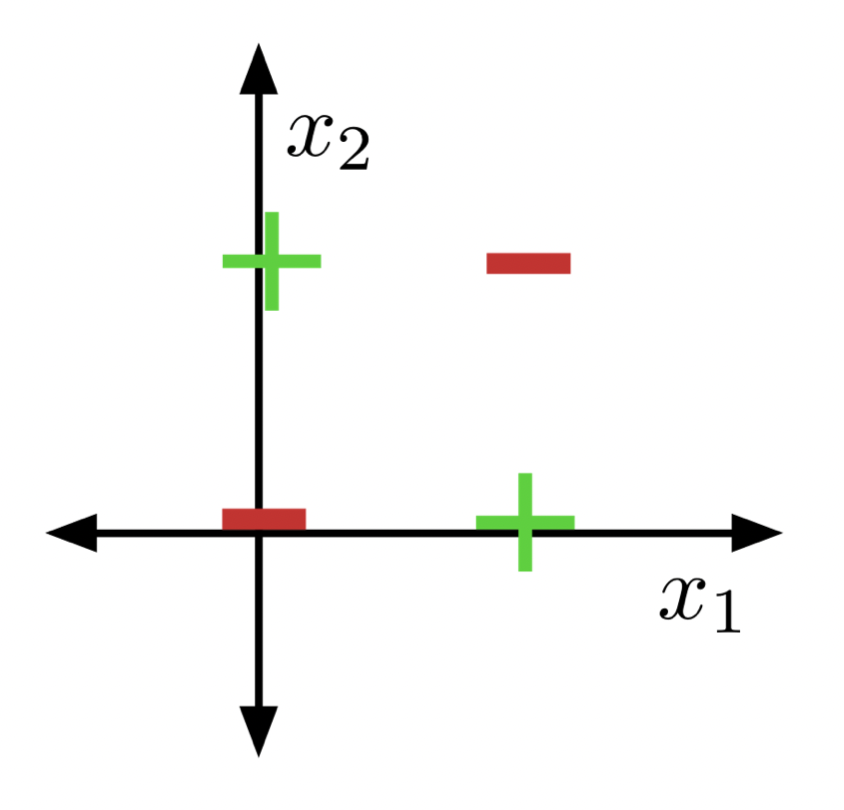
Visually, it is obvious that no line can separate these two classes in the original 2d input space. However, if we add a third dimension to our input feature vector, calculated as $ x_1 x_2 $, then the problem becomes simple! To see why, notice that the only point with a non-zero third dimension value is $ (1, 1) $ which gets lifted above the other 3 points. Then a hyperplane can cut off this lifted point and the origin.

Infinite-Dimensional Feature Spaces and Kernels

The addition of this third dimension can be thought of as a function $ \phi(\cdot) $ that maps an input $ \bx $ to a new feature space. In our XOR example, our $ \phi $ maps:

\[ \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \mapsto \begin{bmatrix} x_1 \\ x_2 \\ x_1x_2 \end{bmatrix} \]

In general many problems that are not linearly separable in the input feature space may be linearly separable in another feature space, as long as we can find the right function $ \phi $. Well, if adding one monomial combination of our vector is good, why not consider an infinite-dimensional feature vector containing every single one? For example: \[ \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \mapsto \begin{bmatrix} x_1 \\ x_2 \\ x_1^2 \\ x_1x_2 \\ x_2^2 \\ x_1^3 \\ x_1^2 x_2 \\ \vdots \end{bmatrix} \] Of course now we have a problem. How are we going to calculate an infinite-dimensional inner product? Before showing how to calculate this, it will be helpful to define what an inner product is.

Given some vector space $\H$ over $\RR$, a function $\langle \cdot, \cdot \rangle_\H : \H \times \H \rightarrow \RR$ is an inner product if it satisfies linearity in the first term, symmetry, and positive definiteness ($\langle f, f \rangle \geq 0$, and $\langle f, f\rangle = 0 \Leftrightarrow f = \mathbf{0}$). A vector space $\H$ with such an inner product is called a Hilbert space². We can now define a kernel as a function $k: \X \times \X \rightarrow \RR$ for which there exists an $\RR$-Hilbert space $\H$ and a map $\phi: \X \rightarrow \H$ such that \[ k(x, x’) := \langle \phi(x), \phi(x’) \rangle \] Notice that we impose no constraints on the set $\X$ other than that it is nonempty. In fact, we don’t even require an inner product to be defined on $\X$ ! As an illustrative example, if $\X$ is a set of documents, then we can define a kernel as long as we can define a feature space that admits an inner product (e.g. a bag of words representation of the text).

Positive Definite Functions

One nice feature of kernels defined this way is that they are positive definite functions. A symmetric function $k: \X \times \X \rightarrow \RR$ is positive definite if, for a set of vectors $(\bx_1, \bx_2, \ldots, \bx_m) \in \RR^n$, the Gram matrix defined as

\[ K := (k(\bx_i, \bx_j))_{ij} \]

is positive semidefinite³, or alternatively \[ \mathbf{c}^\intercal K \mathbf{c} = \sum_{i=1}^m \sum_{j=1}^m c_i c_j k(\bx_i, \bx_j) \geq 0, \quad \forall \mathbf{c} \in \RR^m \] Interestingly, the reverse is also true. Any positive definite function induces a Hilbert space with an inner product over a feature space, even if we do not explicitly define the feature space. For example, consider a function $\phi$ similar to the one above that maps a single input feature to an infinite dimensional vector: \[ x \mapsto \exp\left(-\frac{1}{2}||x||^2\right) \begin{bmatrix} 1 & x & \frac{x^2}{\sqrt{2}} & \frac{x^3}{\sqrt{6}} & \cdots & \frac{x^n}{\sqrt{n!}} & \cdots \end{bmatrix}^\intercal \] Then the inner product $\langle \phi(x), \phi(x’) \rangle$ can be calculated as

\[ \begin{align} \langle \phi(x), \phi(x’) \rangle &= \exp\left(-\frac{1}{2}||x||^2\right)\exp\left(-\frac{1}{2}||x’||^2\right) \sum_{i=0}^\infty \frac{x^i}{\sqrt{i!}} \frac{x’^i}{\sqrt{i!}} \\ &= \exp\left(-\frac{1}{2}||x||^2\right)\exp\left(-\frac{1}{2}||x’||^2\right) \sum_{i=0}^\infty \frac{(xx’)^i}{i!}\\
&= \exp\left(-\frac{1}{2}||x||^2\right)\exp\left(-\frac{1}{2}||x’||^2\right) \exp\left(xx’\right) \\ &= \exp\left(-\frac{1}{2}||x||^2 + xx’ - \frac{1}{2}||x’||^2\right) \\ &= \exp\left(-\frac{1}{2}||x - x’||^2\right) \end{align} \] and we have recovered the Gaussian RBF kernel! This is the essence of the kernel trick, which allows us to train SVMs in infinite dimensional feature spaces (like the one above) without the need to actually create and take inner products of infinite dimensional vectors!

Examples of p.d. Kernels

As shown above, the Gaussian RBF kernel is a positive definite kernel. Consider also the dot product kernel $ k(\bx, \bx’) = \bx^\intercal \bx’$ and the Euclidean distance kernel $ k(\bx, \bx’) = ||\bx - \bx’||^2 $. The dot product kernel is positive definite, since

\[ \begin{align} \sum_{i=1}^m \sum_{j=1}^m c_i c_j \bx_i^\intercal \bx_j &= \sum_{i=1}^m \sum_{j=1}^m c_i c_j \sum_{a=1}^n x_{ia} x_{ja} \\&= \sum_{i=1}^m \sum_{j=1}^m \sum_{a=1}^n c_i x_{ia} c_j x_{ja} \\&= \sum_{a=1}^m \left( \sum_{i=1}^n c_i x_{ia} \right) \left( \sum_{j=1}^n c_j x_{ja} \right)\\&=\sum_{i=1}^n \left( \sum_{i=1}^n c_i x_{ia} \right)^2 \geq 0 \end{align} \]

However, the Euclidean kernel is not. Consider two 2d vectors $ \bx, \bx’ $, such that their Gram matrix is \[ K = \begin{bmatrix} 0 & ||\bx - \bx’|| \\ ||\bx’ - \bx|| & 0 \end{bmatrix} \] If we choose $(1, -1)$ for our $\mathbf{c}$ values, then we get a negative value for $c^\intercal K c$ so the Gram matrix is not positive semidefinite.

The Reproducing Kernel Hilbert Space

So far we have defined positive definite kernels, and shown how they define an inner product in a feature space, even if it is not explcitly defined. Now we can take this one step farther and consider the function space that this kernel induces. We will see that this is called the Reproducing Kernel Hilbert Space.

Let’s go back to our original XOR example. Remember that we had a feature map $\phi$ that transformed: \[ \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \mapsto \begin{bmatrix} x_1 \\ x_2 \\ x_1x_2 \end{bmatrix} \] and we define a positive definite kernel: \[ k(\bx, \by) = \begin{bmatrix} x_1 \\ x_2 \\ x_1x_2 \end{bmatrix}^\intercal \begin{bmatrix} y_1 \\ y_2 \\ y_1y_2 \end{bmatrix} \]

Now let’s define a linear function of these features as $f(\bx) = ax_1 + bx_2 + cx_1x_2$, which maps from $\RR^2 \mapsto \RR$. Since the function is linear, we can represent it nicely as a vector \[ f(\wc) = \begin{bmatrix} a \\ b \\ c \end{bmatrix} \] and evaluate $f(\bx)$ by taking the inner product \[ f(\wc)^\intercal \phi(\bx) := \langle f(\wc), \phi(\bx) \rangle_\H = f(\bx) \] $\H$ here is a Hilbert space of functions mapping $\RR^2 \mapsto \RR$.

One interesting property of representing a function this way is that we can take $\phi$, which normally maps from $\RR^2 \mapsto \RR^3$, and instead use it as the coefficients to define another function! To see how, let’s take the another vector $\by$ with a feature vector defined as before: \[ \phi(\by) = \begin{bmatrix} y_1 \\ y_2 \\ y_1y_2 \end{bmatrix} \] and define a similar linear function $g(\by) = uy_1 + vy_2 + wy_1y_2$. If we set $u = x_1, v = x_2, w = x_1x_2$, then the features from $\phi(x)$ are the coefficients for $g$ and define a function that maps from $\RR^2 \mapsto \RR$. In other words, $\phi(x)$ can be used interchangeably as a function and a feature vector, and the function it defines is precisely our previously defined kernel: \[ \phi(\bx)(\wc) = k(\wc, \bx) \] We can write the pointwise evaluation of this function as $\langle k(\wc, \bx), \phi(\by) \rangle_\H$, and by symmetry, the evaluation of $\phi(\by)(\cdot) = k(\wc, \by)$ as $\langle k(\wc, \by), \phi(\bx) \rangle_\H$. Combining them, we have the property \[ \langle k(\wc, \bx), k(\wc, \by) \rangle = k(\bx, \by) \] We are now ready to define the RKHS.

---

Reproducing Kernel Hilbert Space

Given an arbitrary set $\X$ and a Hilbert space $\H$ of real-valued functions on $\X$, $\H$ is a Reproducing Kernel Hilbert Space (RKHS) if there exists a function $k(\cdot, \cdot) : \X \times \X \rightarrow \RR$, called the reproducing kernel, such that

1. $\forall x \in \X,\ k(\cdot, x) \in \H$
2. $\forall x \in \X,\ \forall f \in \H,\ \langle f, k(\cdot, x) \rangle_\H = f(x)$ (the reproducing property)

In particular, this means that for any $x, y \in \RR$, we have $k(x, y) = \langle k(\cdot, x),\ k(\cdot, y) \rangle_\H$

---

A Concrete Example

RKHSs are a bit abstract to think about, so let’s look at an even simpler example. Let’s consider an input space $\X = \RR$ and a dot product kernel $k(x, x’) = \langle \phi(x), \phi(x’) \rangle$ where $\phi(x) = \begin{bmatrix} 1 & x & x^2 & x^3 \end{bmatrix}^\intercal$. What is the RKHS $\H$ defined by $k$? Since our kernel combines monomial features of up to degree 3 linearly, $\H$ is simply the space of all polynomials of degree 3!

Note that $\H$ is larger than the set of possible feature vectors ${x \in \phi(x)}$. As an example, consider the function $f(x) = 1 - 2x^2$. The vector associated with this function, $\begin{bmatrix} 1 & 0 & -2 & 0 \end{bmatrix}^\intercal$ is not in the image of $\phi(\cdot)$ since it would require $x^2 = -2$. Of course we could expand $\X$ to include the complex numbers, but that’s a story for another day…

Norms and Evaluation Operators

Since an RKHS is endowed with an inner product, it also admits a norm: \[ ||f||_\H = \sqrt{\langle f, f \rangle} \] A small norm value implies smoothness, and regularizing the norm is a common method of restricting the learned function space of a model. This norm is also useful in a second definition of an RKHS, states that the evluation operator is linearly bounded. The evaluation operator $\delta_x$ evaluates a function $f$ at $x$, i.e. $\delta_x f = f(x)$, and it is linearly bounded when \[ \delta_x f \leq \lambda_x || f ||_\H,\ \lambda_x \geq 0 \] Proving this fact is relatively straightforward and uses most of the things we’ve learned thus far. It might be instructional to try it yourself, but if that doesn’t sound like your definition of fun, I’ve also provided it below.

Proof

\[ \begin{aligned} |\delta_x f | &= |f(x)| \\ &= |\langle f, k(\cdot, x) \rangle_\H| \\ &\leq ||k(\cdot, x)||_\H ||f||_\H \\ &= \sqrt{\langle k(\cdot, x), k(\cdot, x) \rangle_\H} ||f||_\H \\ &= \sqrt{k(x, x)} ||f||_\H \end{aligned} \] The third line follows from Cauchy-Schwarz.

What this means is that two functions in an RKHS are identical if they agree at every point $x$. \[ |f(x) - g(x)| = |\delta_x f - \delta_x g| = |\delta_x (f - g)| \leq \lambda_x ||f - g||_\H \] This is a useful property when we are optimizing some function $f \in \H$, since closeness in RKHS space implies closeness everywhere in input space.

Conclusion

We have learned about feature spaces and shown how a positive definite kernel can implicitly define an infinite dimensional feature space. These kernels also define an RKHS with the reproducing property that evaluation can be performed with inner products. RKHSs have nice properties that make them useful for general learning algorithms.

---